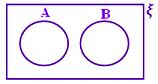
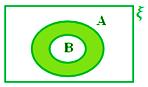
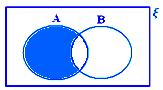
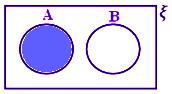
Relationship in Sets using Venn Diagram

The relationship in sets using Venn diagram are discussed below:

• The union of two sets can be represented by Venn diagrams by the shaded region, representing A ∪ B.

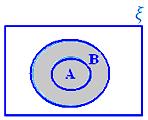
A ∪ B when A ⊂ B

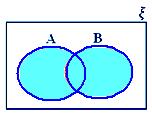
A ∪ B when neither A ⊂ B nor B ⊂ A

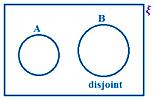
A ∪ B when A and B are disjoint sets

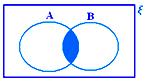
• The intersection of two sets can be represented by Venn diagram, with the shaded region representing A ∩ B.

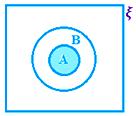
A ∩ B when A ⊂ B, i.e., A ∩ B = A

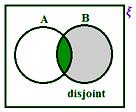
A ∩ B when neither A ⊂ B nor B ⊂ A

A ∩ B = ϕ No shaded part

• The difference of two sets can be represented by Venn diagrams, with the shaded region representing A – B.

A – B when neither A ⊂ B nor B ⊂ A

A – B when A and B are disjoint sets.

Here A – B = A

A – B when A ⊂ B

Here A – B = ϕ

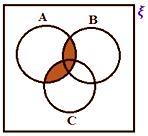
Relationship between the three Sets using Venn Diagram

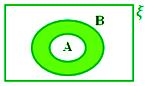
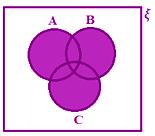
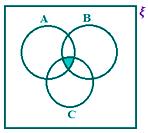
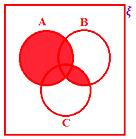
• If ξ represents the universal set and A, B, C are the three subsets of the universal sets. Here, all the three sets are overlapping sets.

Let us learn to represent various operations on these sets.

A ∪ B ∪ C

A ∩ B ∩ C

Some important results on number of elements in sets and their use in practical problems.

Now, we shall learn the utility of set theory in practical problems.

If A is a finite set, then the number of elements in A is denoted by n(A).

Relationship in Sets using Venn Diagram
Let A and B be two finite sets, then two cases arise:

Case 1:

A and B are disjoint.

Here, we observe that there is no common element in A and B.

Therefore, n(A ∪ B) = n(A) + n(B)

Case 2:

When A and B are not disjoint, we have from the figure

(i) n(A ∪ B) = n(A) + n(B) – n(A ∩ B)

(ii) n(A ∪ B) = n(A – B) + n(B – A) + n(A ∩ B)

(iii) n(A) = n(A – B) + n(A ∩ B)

(iv) n(B) = n(B – A) + n(A ∩ B)

A – B

B – A

A ∩ B

Let A, B, C be any three finite sets, then

n(A ∪ B ∪ C) = n[(A ∪ B) ∪ C]

= n(A ∪ B) + n(C) – n[(A ∪ B) ∩ C]

= [n(A) + n(B) – n(A ∩ B)] + n(C) – n [(A ∩ C) ∪ (B ∩ C)]

= n(A) + n(B) + n(C) – n(A ∩ B) – n(A ∩ C) – n(B ∩ C) + n(A ∩ B ∩ C)

[Since, (A ∩ C) ∩ (B ∩ C) = A ∩ B ∩ C]

Therefore, n(A ∪B ∪ C) = n(A) + n(B) + n(C) – n(A ∩ B) – n(B ∩ C) – n(C ∩ A) + n(A ∩ B ∩ C)