Union of Sets using Venn Diagram

The union set operations can be visualized from the diagrammatic representation
of sets.

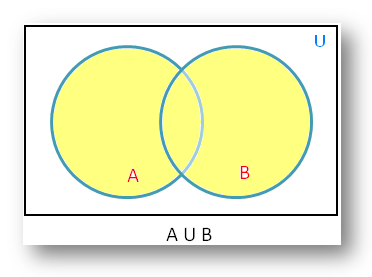
The rectangular region represents the universal set U and
the circular regions the subsets A and B. The shaded portion represents the set
name below the diagram.

Let A and B be the two sets. The union of A and B is the set
of all those elements which belong either to A or to B or both A and B.

Now we will use the notation A U B (which is read as ‘A
union B’) to denote the union of set A and set B.

Thus, A U B = {x : x ∈ A or x ∈ B}.

Clearly, x ∈ A U
B   

⇒ x ∈ A or x ∈ B

Similarly, if x ∉ A U B

⇒ x ∉ A or x ∉ B

Therefore, the shaded portion in the adjoining figure represents A U B.

Thus, we conclude from the definition of union of sets that
A ⊆
A U B, B ⊆ A U B.

From the above Venn diagram the following theorems are obvious:

(i) A ∪ A = A                        (Idempotent theorem)

(ii) A ⋃ U = U                       (Theorem of ⋃) U is the universal set.

(iii) If A ⊆ B, then A ⋃ B = B

(iv) A ∪ B = B ∪ A                (Commutative theorem)

(v) A ∪ ϕ = A                      (Theorem of identity element, is the identity of ∪) 

(vi) A ⋃ A’ = U                     (Theorem of ⋃) U is the universal set.

Notes:

A ∪ ϕ = ϕ ∪ A = A i.e. union of any set with the empty set is always the set itself.

Solved examples of union of sets using Venn diagram:

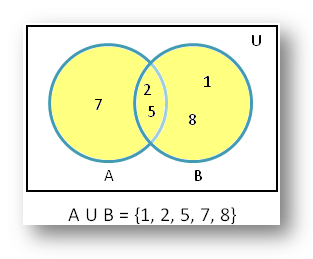
1. If A = {2, 5, 7} and B = {1, 2, 5, 8}. Find A U B using venn diagram.

Solution:

According to the given question we know, A = {2, 5, 7} and B = {1, 2, 5, 8}

Now let’s draw the venn diagram to find A union B.

Therefore, from the Venn diagram we get A U B = {1, 2, 5, 7,
8}

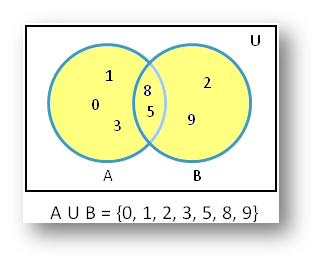
2. From the
adjoining figure find A union B.

Solution:

According to the adjoining figure we get;

Set A = {0, 1, 3, 5, 8}

Set B = {2, 5, 8, 9}

Therefore, A union B is the set of elements which in set A
or in set B or in both.

Thus, A U B = {0, 1, 2, 3, 5, 8, 9}