The intersection of Sets using Venn Diagram

Learn how to represent the
intersection of sets using Venn diagram. The intersection set operations can be
visualized from the diagrammatic representation of sets.

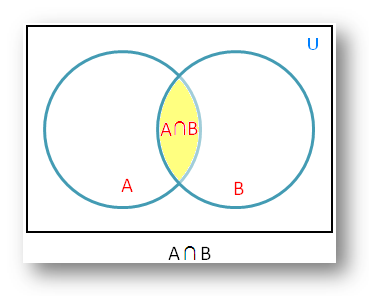
The rectangular region
represents the universal set U and the circular regions the subsets A and B.
The shaded portion represents the set name below the diagram.

Let A and B be the two
sets. The intersection of A and B is the set of all those elements which belong
to both A and B.

Now we will use the notation
A ∩ B (which
is read as ‘A intersection B’) to denote the intersection of set A and set B.

Thus, A ∩ B = {x : x ∈ A and x ∈ B}.

Clearly, x ∈ A ∩ B   

⇒ x ∈ A and x ∈ B

Therefore, the shaded portion in the adjoining figure represents A ∩ B.

Thus, we conclude from the definition of intersection of sets that A ∩ B ⊆ A, A ∩ B ⊆ B.

From the above Venn diagram the following theorems are obvious:

(i) A ∩ A = A                        (Idempotent theorem)

(ii) A ∩ U = A                       (Theorem of union)

(iii) If A ⊆ B, then A ∩ B = A.

(iv) A ∩ B = B ∩ A                 (Commutative theorem)

(v) A ∩ ϕ = ϕ                       (Theorem of ϕ)

(vi) A ∩ A’ = ϕ                      (Theorem of ϕ)

The symbols ⋃ and ∩ are often read as ‘cup’ and ‘cap’ respectively.

For two disjoint sets A and B, A ∩ B = ϕ.

Solved examples of
intersection of sets using Venn diagram:

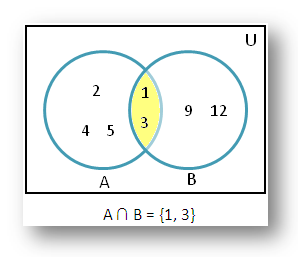
1. If A = {1, 2, 3, 4, 5} and B = {1, 3, 9, 12}. Find A ∩ B using
venn diagram.

Solution:

According to the given
question we know, A = {1, 2, 3, 4, 5} and B = {1, 3, 9, 12}

Now let’s draw the venn
diagram to find A intersection B.

Therefore, from the venn
diagram we get A ∩ B = {1,
3}

2. From
the adjoining figure find A intersection
B.

Solution:

According to the adjoining figure we get;

Set A = {m, p, q, r, s, t, u, v}

Set B = {m, n, o, p, q, i, j, k, g}

Therefore, A intersection B
is the set of elements which belong to both set
A and set B.

Thus, A
∩ B = {p, q, m}