Symmetric Difference using Venn Diagram

The symmetric difference using Venn diagram
of two subsets A and B is a sub set of U, denoted by A △ B and is defined by

A △ B = (A – B) ∪ (B – A)

Let A and B are two sets. The symmetric
difference of two sets A and B is the set (A – B) ∪ (B – A) and is denoted
by A △ B.

Thus,
A △ B = (A – B) ∪ (B – A) = {x : x ∉ A ∩ B}

or,
A △ B = {x : [x ∈ A and x ∉ B] or [x ∈ B and x ∉ A]}

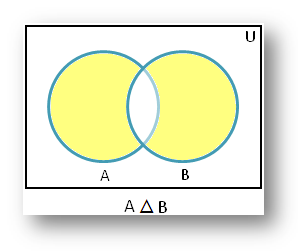
The shaded part of the given Venn diagram represents A △ B.

A △ B is
the set of all those elements which belongs either to A or to B but not to
both.

A △ B is
also expressed by (A ∪ B) –
(B ∩ A).

It
follows that A △ ∅ = A for all subset A,

A △ A = ∅ for all subset A

Properties of symmetric difference:

(i) A
△ B =
B △ A;                                       [Commutative
property]

(ii)
A △ (B △ C) =
(A △ B) △ C                       [Associative
property]

Example to find the symmetric
difference using Venn diagram:

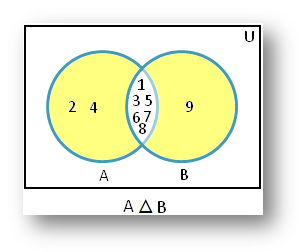
1. If A = {1, 2, 3, 4, 5, 6, 7, 8} and B =
{1, 3, 5, 6, 7, 8, 9}, then A – B = {2, 4}, B – A = {9} and A △ B = {2, 4, 9}.

Therefore,
the shaded part of the Venn diagram represents A △ B = {2, 4, 9}.

2. If A = {1, 2, 4, 7, 9} and B = {2, 3, 7, 8, 9} then A △ B = {1, 3, 4, 8}

Therefore,
the shaded part of the Venn diagram represents A △ B = {1, 3, 4, 8}.

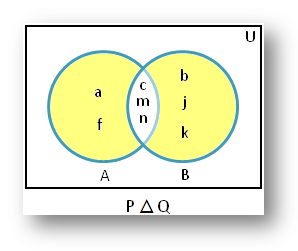
3. If P = {a, c, f, m, n} and Q = {b, c, m, n, j, k} then P △ Q = {a, b, f, j, k}

Therefore,
the shaded part of the Venn diagram represents P △ Q = {a, b, f, j, k}.