powers (exponents):

A power
contains two parts exponent and base.

We know 2 × 2 × 2 × 2 = 2⁴, where 2 is called the base and 4 is called the power or exponent or index of 2.

Reading Exponents

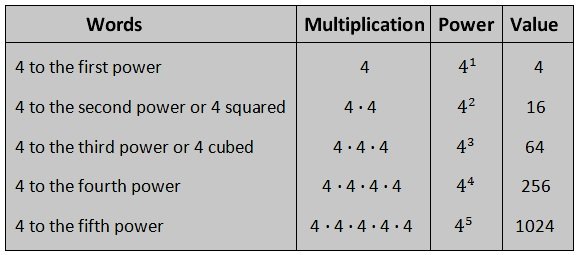
Examples on evaluating powers (exponents):

(i) 5⁴.

Solution:

5⁴
= 5 ∙ 5 ∙ 5 ∙ 5           → Use 5 as a factor 4 times.
= 625                     → Multiply.

(ii) (-3)³.

Solution:

(-3)³
= (-3) ∙ (-3) ∙ (-3)          → Use -3 as a factor 3 times.
= -27                            → Multiply.

(iii) -7².

Solution:

-7²
= -(7²)             → The power is only for 7 not for negative 7
= -(7 ∙ 7)          → Use 7 as a factor 2 times.
= -(49)             → Multiply.
= -49

(iv) (2/5)³

Solution:

(2/5)³
= (2/5) ∙ (2/5) ∙ (2/5)           → Use 2/5 as a factor 3 times.
= 8/125                              → Multiply the fractions

Writing Powers (exponents)

2.
Write each number as the power of a given base:

(a) 16; base 2

Solution:

16; base 2
Express 16 as an exponential form where base is 2
The product of four 2’s is 16.
Therefore, 16
= 2 ∙ 2 ∙ 2 ∙ 2
= 2⁴
Therefore, required form = 2⁴

(b) 81; base -3

Solution:

81; base -3
Express 81 as an exponential form where base is -3
The product of four (-3)’s is 81.
Therefore, 81
= (-3) ∙ (-3) ∙ (-3) ∙ (-3)
= (-3)⁴
Therefore, required form = (-3)⁴

(c) -343; base -7

Solution:

-343; base -7
Express -343 as an exponential form where base is -7
The product of three (-7)’s is -343.
Therefore, -343
= (-7) ∙ (-7) ∙ (-7)
= (-7)³
Therefore, required form = (-7)³