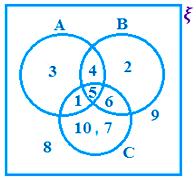
Examples on Venn Diagram

From the adjoining Venn diagram, find the following sets.

(i) A

(ii) B

(iii) ξ

(iv) A’

(v) B’

(vi) C’

(vii) C – A

(viii) B – C

(ix) A – B

(x) A ∪ B

(xi) B ∪ C

(xii) A ∩ C

(xiii) B ∩ C

(xiv) (B ∪ C)’

(xv) (A ∩ B)’

(xvi) (A ∪ B) ∩ C

(xvii) A ∩ (B ∩ C)

Answers for examples on Venn diagram are given below:

(i) A

= {1, 3, 4, 5}

(ii) B

= {4, 5, 6, 2}

(iii) ξ

= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}

(iv) A’

= {2, 6, 7, 8, 9, 10}     all elements of universal set leaving the elements of set A.

(v) B’

= {1, 3, 7, 8, 9, 10}     all elements of universal set leaving the elements of set B.

(vi) C’ = To find

C = {1, 5, 6, 7, 10}

Therefore, C’ = {2, 3, 4, 8, 9}     all elements of universal set leaving the elements of set C.

(vii) C – A

Here C = {1, 5, 6, 7, 10}

A = {1, 3, 4, 5}

then C – A = {6, 7, 10}     excluding all elements of A from C.

(viii) B – C

Here B = {4, 5, 6, 2}

C = {1, 5, 6, 7, 10}

B – C = {4, 2}     excluding all elements of C from B.

(ix) B – A

Here B = {4, 5, 2}

A = {1, 3, 4, 5}

B – A = {6, 2}     excluding all elements of A from C. 

(x) A ∪ B

Here A = {1, 3, 4, 5}

B = (4, 5, 6, 2}

A ∪ B = {1, 2, 3, 4, 5, 6}

(xi) B ∪ C

Here B = {4, 5, 6, 2}

C = {1, 5, 6, 7, 10}

B ∪ C = {1, 2, 4, 5, 6, 7, 10}

(xii) (B ∪ C)’

Since, B ∪ C = {1, 2, 4, 5, 6, 7, 10}

Therefore, (B ∪ C)’ = {3, 8, 9}

(xiii) (A ∩ B)’ 

A = {1, 3, 4, 5}

B = {4, 5, 6, 2}

(A ∩ B) = {4, 5}

(A ∩ B)’ = {1, 2, 3, 6, 7, 8, 9, 10}

(xiv) (A ∪ B) ∩ C

A = {1, 2, 3, 4}

B = {4, 5, 6, 2}

C = {1, 5, 6, 7, 10}

A ∪ B= {1, 2, 3, 4, 5, 6}

(A ∪ B) ∩ C = {1, 5, 6}

(xv) A ∩ (B ∩ C) 

A = {1, 3, 4, 5}

B = {4, 5, 6, 2}

C = {1, 5, 6, 7, 10}

B ∩ C = {5, 6}

A ∩ (B ∩ C) = {5}