Complement of a Set using Venn Diagram

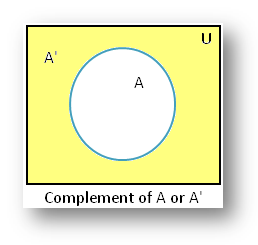
The complement of a set using Venn diagram is a subset of
U. Let U be the universal set and let A be a set such that A ⊂
U. Then,
the complement of A with respect to U is denoted by A’ or AC

C or U – A
or ~ A and is defined the set of all those
elements of U which are not in A.

Thus, A’ =
{x ∈ U : x ∉ A}.

Clearly, x ∈ A’ ⇒ x ∉ A

(A – B) is also called the complement of B relative to A. From
the definition it is clear that the complement of the whole set in a set is the
null set; for U’ = U – U = ∅ again ∅’ = U – ∅ = U also (A’)’ = U – A’ = U – (U
– A) = A. If the set of real numbers be the universal set, then the set of
rational numbers and the set of irrational numbers are complements of each
other. 

Example on complement of a set
using Venn diagram:

1. Let
the set of natural numbers N = {1, 2, 3, ………..} be the universal set and let A
= {2, 4, 6, 8, ……….}

Then A’ =
{1, 3, 5, ………}

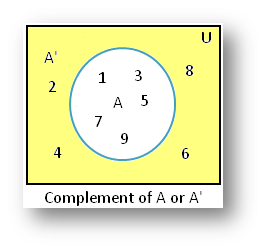
2. If U = {1, 2, 3, 4, 5, 6, 7, 8, 9}
and A = {1, 3, 5, 7, 9} then A’ = {2, 4, 6, 8}

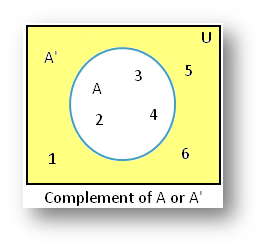
3. If U = {1, 2, 3, 4, 5, 6} and A =
{2, 3, 4} then U – A = ~ A = A’ = {1, 5, 6}.

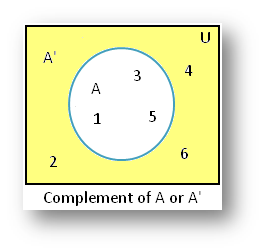
4. U = {1, 2, 3, 4, 5, 6} be the universal set and A = {1,
3, 5} then A’ = {2, 4, 6}.

Properties of complement
of a set:

1. U’ = ∅

2. ∅’ = U

3. A U A’ = U        For
any subset A

4. A ∩ A’ = ∅        For any subset A

5. (A’)’ = A          For
any subset A.